
"It's a famous paradox that has a solution that is so absurd,
most people refuse to believe it's true."
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, and shows you that there is a goat behind it. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice? (From Parade magazine’s Ask Marilyn column) Or in a more general way, instead of just 3 doors imagine you're given N doors and the host opens N-2 doors after you make your choice, leaving you with the choice that you made initially and just one other. Now, if you/re asked to stay on your choice or switch what will you do? Do you stay or switch? Which will be the better option? You should always switch. But why?
Objective
In this project I simulate the problem and experimentally show how this "counter-intuitive" solution is actually correct. I also tackle some of the other questions that arise from the same problem, namely -
- What will happen if we have N doors and the host opens N-2 doors after we have made our initial choice? How often will we win if we switch? (i.e. what is the probability of winning)
- What will happen if we have a constant number of doors, say 100, and k (less than 100) doors are opened? How often will we win if we switch? (i.e. what is the probability of winning)
Result
- As the number of doors N increase the probability of winning also increases. And when N = ∞ the winning probability becomes equal to 1.
- As the number of doors opened k increase the probability of winning also increases but slowly. And when k = 98; the winning probability becomes equal to 0.99.
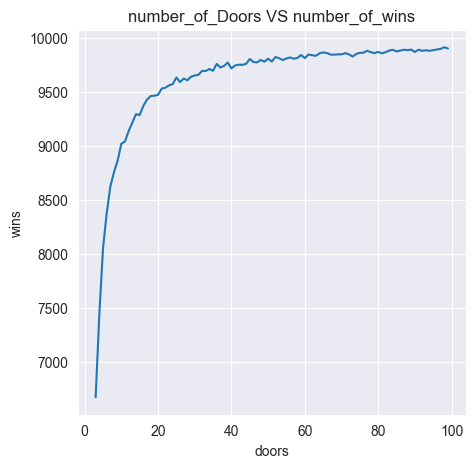
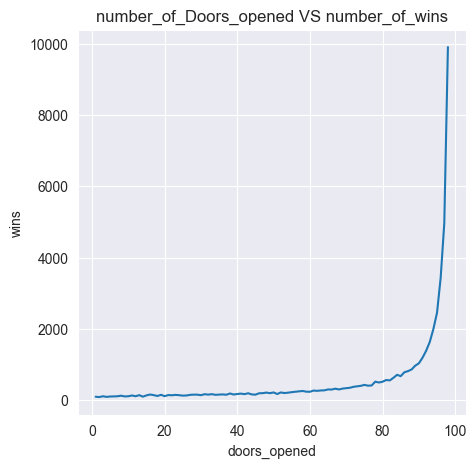
The theoretical explanation of the correctness of these results is explained in an article authored by me, link for which is given below.
